반응형
경사하강법에 대해 Araboza
최적화 문제를 다루기 위해 목적함수를 설정하고 우리는 목적함수(손실함수)의 손실을 최소화가 필요하다
이 때 경사하강법을 사용할 수 있따!
경사하강법은 기울기 변화를 통해 함수의 최솟값을 찾는 알고리즘이다
- 먼저 경사하강법에 대해 알기 위해 미분의 개념이 필요하다
- Def) 미분(Differential)
- 어떤 운동이나 함수의 순간적인 움직임을 서술하는 방법, 그것의 도함수를 도출해내는 과정으로 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구로 최적화에 자주 쓰임
- 아래는 파이썬의 sympy 라이브러리를 이용한 미분계산 과정이다
import sympy
from sympy.abc import x
sym.diff(sym.ply(x**3 + 3*x**2 + 3 ), x)- 다변수 함수의 편미분
import sympys as sym
from sympy.abc import x, y
sym.diff(sym.poly(x**2 + 2*x*y +3) + sym.cos(x + 2*y))- 한 점에서 접선의 기울기를 알면 어느 방향으로 점을 움직여야 함수값이 증가/감소 하는지 알 수 있다
- 미분값을 더하면 => 증가
- 미분값을 빼면 => 감소
- 기울기가 음수인 경우를 생각해보자, 이 때 기울기를 더하면 왼쪽방향으로 이동을 할 것 이고 기울기가 음수라는 것은 왼쪽의 함수값이 더 높다는 것을 뜻하기 때문에 기울기를 더하게 되면 함수값이 증가한다. 양수일 때도 similarly!
- 미분값을 더하면서 함수의 극대값의 위치를 구하는 방법을 경사상승법(Gradient ascent)이라 한다
- 반대로 미분값을 빼면서 함수의 극소값의 위치를 구하는 방법은 경사하강법(Gradient descent)라 한다. 즉, 이를 통해 목적함수를 최소화할 수 있다 !
- 위와 같이 더하거나 빼면서 함수값을 조정하고 극값(미분값이 0이 되는 지점)에서 최적화가 완료된다.
- 아래는 알고리즘 수도코드이다.
# Input : gradient, init(시작점), lr, eps
# Output : var
var = init
grad = gradient(var)
while abs(grad) > eps: # 컴퓨터로 계산할 때 미분값이 0이 되는경우는 거의 없어 종료조건을 설정해야됨, 2차원 이상이라면 절대값 대신 norm을 사용
var = var - lr * grad # lr : 학습률로 업데이트하는 속도를 조절
grad = gradient(var) # 계속해서 미분값 업데이트 - 차원이 높아졌을 때는 각 변수 별로 편미분을 계산한 gradient 벡터를 이용하여 경사하강/상승법을 사용한다.
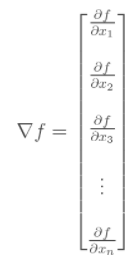
Gradient Vector : 벡터 미적분학에서 스칼라장의 최대의 증가율을 나타내는 벡터장을 뜻한다. 따라서 최대값, 최소값을 찾는데 사용할 수 있다.
경사하강법으로 선형회귀 계수 구하기
- 선형회귀의 목적식은 아래와 같다.
- $${||y-X\beta||_2} \quad 또는 \;\; {||y-X\beta||^2_2}$$를 사용시 계산이 편리하다
- 이 때 최소화 하는 Beta를 찾기 위해 아래와 같은 gradient vector를 구해야 한다. ($$y \text{와}\; \hat y\text{를 최소화 해주는게 목표!}$$)
$$\nabla_\beta||y-X\beta||_2 = - { X^T(y-X\beta)\over n||y-X\beta||_2 }$$
- 아래의 내용을 잘 계산하면 위와 같은 결과가 나온다..........

- 따라서 목적식 Beta를 구하는 경사하강법 알고리즘은 아래와 같다
$$\beta^{(t+1)} = \beta^{(t)} - \lambda\nabla_\beta||y-X\beta^{t}||=\beta^{(t)}+ { \lambda X^T(y-X\beta)\over n||y-X\beta||_2 }$$
- 제곱을 사용한다면 아래와 같다
$$\beta^{(t+1)} = \beta^{(t)} + {2\lambda\over n}X^T(y-X\beta^{t})$$
- 아래는 수도코드를 이용한 알고리즘 이다
for t in range(T):
error = y - X @ beta
grad = -transpose(X) @ error
beta = beta - lr * grad- 앞서 pesudo-inverse를 이용하여 구한 것과 달리 경사하강법을 사용할시 학습률(lr), 학습횟수가 중요한 hyperparameter로 작용한다.
🤔 그런데, 과연 경사하강법은 만능일까?
- 이론적으로 미분가능하고 볼록(convex)한 함수에 대해서는 수렴이 보장된다, 그러나 우리가 주로 마주치게될 많은 함수는 non-convex라서 곤.란. 또한 데이터가 메모리의 문제 또한 발생할 수 있다
- 이를 극복하기 위해 확률적경사하강법(StochasticGradientDescent, SGD)가 존재한다
- 기존에 모든 데이터를 이용해 업데이트하는 방식에서 확률적으로 일부분(mini-batch)만을 선택하여 업데이트하는 방식으로 기존의 문제점을 극복하였다
- 이는 전체데이터를 사용할 때의 gradient의 결과는 비슷하고 연산량을 대폭감소시킨다(데이터 전체가 아닌 일부분만을 사용하므로!)
- Gradient Desent 는
$$\ {D = (X,y)}\text{를 통해} \nabla_\theta L(D,\theta)\text{를 계산}$$
- SGD는 mini-batch를 활용해 아래와 같이 gradient를 계산한다.
$$D_{(b)}=(X_{(b)},y_{(b)}) \subset D$$
- 이 때 mini-batch는 확률적으로 선택되기 때문에 매번 목적식 모양이 다를 수 있다
반응형
'⚡AI > ∃Mathematics' 카테고리의 다른 글
| 공분산과 상관계수 (0) | 2022.02.03 |
|---|---|
| 딥러닝을 위한 통계학 맛보기 (0) | 2022.01.21 |
| 딥러닝을 위한 확률론 맛보기 (0) | 2022.01.21 |
| 딥러닝 학습방법(비선형모델 학습) (0) | 2022.01.20 |
| 벡터&행렬이란 무엇인가? (0) | 2022.01.17 |