딥러닝에서 확률론이 필요한 이유는 무엇일까?
- 딥러닝은 확률론 기반의 기계학습 이론에 바탕을 두기 때문
- 손실함수(loss function)들의 작동 원리는 데이터 공간을 통계적으로 해석해서 유도하기 떄문
우리의 목표는 결국 정답을 맞추는 것인데 예측이 틀릴 위험을 최소화하려면 통계적 기계학습의 방법을 사용해야한다.
- 이에 대한 예시는 다음과 같으며 이는 오차 또는 불확실성을 최소화하도록 유도한다
- 회귀분석에서 사용되는 loss func으로 사용되는 L2
- 분류 문제에서 사용되는 cross-entropy
- 결국 분산 및 불확실성을 최소화하기위해서는 기준을 세워야 하고 이를 측정하는 방법을 알아야한다
- 이 때, 두 대상을 측정하는 방법을 통계학에서 제공한다!
확률변수
- 확률변수는 확률분포에 따라 이산형(discrete)과 연속형(continuous)로 나뉜다
- (변수는 데이터공간이아닌 분포에 의해서 결정된다!)
- 사실 엄밀히 따지면 이산, 연속 딱 두종류로만 나눠지지는 않는다
- 이산형 확률변수는 확률변수가 가질 수 있는 경우의 수를 모두 고려하여 확률을 더해서 모델링한다
- 연속형 확률변수는 데이터 공간에 정의된 확률변수의 밀도(density) 위에서의 적분을 통해 모델링한다
확률 분포
- 데이터는 확률변수로 (x, y) ~ D라 표기한다.
- D는 이론적으로 존재하는 확률분포이기 때문에 사전에 알 수 없다.
- 결합분포 P(x, y)는 D를 모델링한다
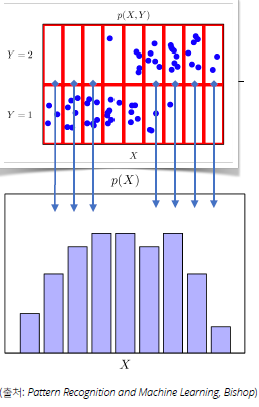
- P(x)는 입력 x에 대한 주변확률분포로 y에 대한 정보를 제공하지는 않는다
-
P(x),\text{(주변확률분포)} : f_x(x) \text{Marginal PDF, PMF 말하는 거!}
- 조건부확률분포 P(x|y)는 데이터 공간에서 입력 x와 출력 y사이의 관계를 모델링한다, 또한 주변확률 분포보 조건부확률분포를 사용하는게 좀 더 명확하다
- 조건부확률 P(y|x)는 입력변수 x에 대해 정답이 y일 확률을 의미하며 연속확률분포의 경우 밀도로 해석된다
- 선형모델과 소프트맥스 함수의 결합은 데이터에서 추출된 패턴을 기반으로 확률을 해석하는데 사용된다
-
$$\text{분류문제에서 } softmax(W\phi + b)\text{은 데이터 x로 부터 추출된 특징 패턴} \phi(x) \text{과 가중치행렬 W을 통해 조건부확률} \\ P(y|x) \text{을 계산한다.}$$
- 회귀문제의 경우 연속이라 밀도를 사용하며 조건부기대값 E[y|x]을 추정한다
- 이는 L2 norm을 최소화하는 함수와 일치한다!
- 딥러닝은 다층신경망을 사용하여 데이터로부터 특징패턴을 추출한다
- 이 때 특징패턴을 학습하기 위해 어떤 loss func을 선택할지는 기계학습 문제와 모델에 의해 결정된다
몬테카를로 샘플링
- ML에서 많은 문제들은 확률분포를 모르는 경우가 대부분이다
- 이 때, <b>데이터를 이용하여 기대값을 계산하려면 몬테카를로(Monte Carlo)샘플링을 사용</b>한다(이산형이든 연속형이든 관계 x)
- 몬테카를로 샘플링은 독립추출만 보장된다면 대수의 법칙(law of large number)에 의해 수렴성을 보장한다.

Markov Chain과 연결되어있는 내용같은데 관련해서 알아봐야게땅
반응형
'⚡AI > ∃Mathematics' 카테고리의 다른 글
| 공분산과 상관계수 (0) | 2022.02.03 |
|---|---|
| 딥러닝을 위한 통계학 맛보기 (0) | 2022.01.21 |
| 딥러닝 학습방법(비선형모델 학습) (0) | 2022.01.20 |
| 경사하강법(Gradient Decent) (0) | 2022.01.19 |
| 벡터&행렬이란 무엇인가? (0) | 2022.01.17 |