조건부 확률은 무엇인가요?
- 사건 A가 일어났다는 전제 하에 사건 B가 일어날 확률
$$ P(B|A) = P(B \cap A) / P(A) $$
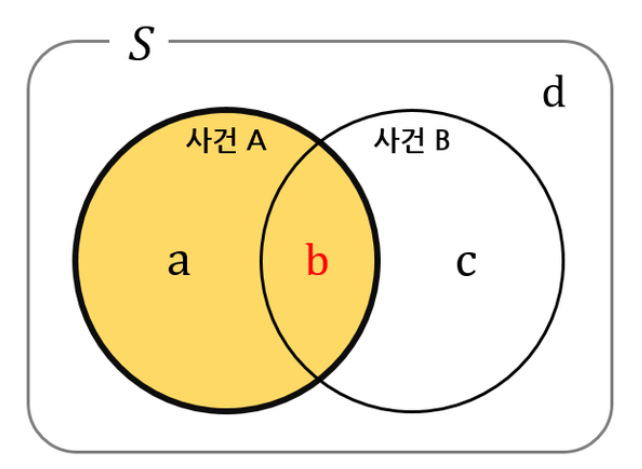
이 조건부 확률은 베이즈 정리와도 이어져 매우매우 중요함!
베이즈 정리
- 데이터라는 조건이 주어졌을 때의 조건부확률을 구하는 공식
- 데이터가 주어지기 전의 사전확률 값이 데이터가 주어지면 어떻게 변하는지 계산할 수 있다
- 따라서 데이터가 주어지기 전에 이미 어느 정도 확률 값을 예측하고 있을 때 이를 새로 수집한 데이터와 합쳐서 최종 결과에 반영할수 있다
- 이는 데이터의 개수가 부족할 경우 아주 유용하고 데이터를 매일 추가적으로 얻는 상황에서도 매일 전체 데이터를 대상으로 새로 분석작업을 할 필요없이 어제분석결과에 오늘 들어온 데이터를 합쳐서 업데이트만 하면 되므로 유용하게 활용 가능

- 참고
반응형
'⚡AI > ∃Mathematics' 카테고리의 다른 글
| 누적분포 함수와 확률밀도 함수 (0) | 2022.03.17 |
|---|---|
| 확률변수와 확률모형 (0) | 2022.03.16 |
| 샘플링과 리샘플링 (0) | 2022.03.16 |
| eigen vector & eigenvalue (0) | 2022.03.16 |
| 공분산과 상관계수 (0) | 2022.02.03 |
